Cách xác định nhanh góc giữa hai đường thẳng chéo nhau – Công thức và bài tập có đáp án chi tiết - Tự Học 365

Cách xác toan thời gian nhanh góc đằm thắm hai tuyến đường trực tiếp chéo cánh nhau – Công thức và bài bác tập luyện với đáp án

1. Định nghĩa góc đằm thắm hai tuyến đường thẳng

Trong không khí cho tới 2 đường thẳng liền mạch a, b ngẫu nhiên.

Từ một điểm O nào là cơ tớ vẽ 2 đường thẳng liền mạch ${a}'$, ${b}'$ theo thứ tự tuy vậy song với a và b. Ta nhận biết rằng khi điểm O thay cho thay đổi thì góc đằm thắm 2 đường thẳng liền mạch ${a}'$ và ${b}'$ bất biến.

Bạn đang xem: Cách xác định nhanh góc giữa hai đường thẳng chéo nhau – Công thức và bài tập có đáp án chi tiết - Tự Học 365

Do cơ tớ với toan nghĩa:

Định nghĩa: Góc đằm thắm 2 đường thẳng liền mạch a và b vô không khí là góc đằm thắm 2 đường thẳng liền mạch ${a}'$ và ${b}'$ nằm trong trải qua một điểm và theo thứ tự tuy vậy song với a và b.

2. Cách xác lập góc đằm thắm hai tuyến đường thẳng

Để xác lập góc đằm thắm 2 đường thẳng liền mạch a và b tớ hoàn toàn có thể lấy điểm O nằm trong 1 trong hai tuyến đường trực tiếp cơ rồi vẽ một đường thẳng liền mạch qua quýt O và tuy vậy song với đường thẳng liền mạch còn sót lại.

Nếu $\overrightarrow{u}$ là vecto chỉ phương của đường thẳng liền mạch a và $\overrightarrow{v}$ là vecto chỉ phương của đường thẳng liền mạch b và $\left( \overrightarrow{u};\overrightarrow{v} \right)=\alpha $ thì góc đằm thắm 2 đường thẳng liền mạch a và b bởi vì $\alpha $ nếu như $0\le \alpha \le 90{}^\circ $ và bởi vì $180{}^\circ -\alpha $ nếu như $90{}^\circ <\alpha \le 180{}^\circ $. Nếu 2 đường thẳng liền mạch a và b tuy vậy song hoặc trùng nhau thì góc đằm thắm bọn chúng bởi vì $0{}^\circ $. Góc đằm thắm 2 đường thẳng liền mạch là góc với số đo $0\le \alpha \le 90{}^\circ $.

3. Phương pháp tính góc đằm thắm hai tuyến đường thẳng

Để tính góc đằm thắm hai tuyến đường trực tiếp vô không khí tất cả chúng ta lưu ý những công thức sau:

■ Định lý hàm số cosin vô tam giác ABC: $\cos \widehat{BAC}=\frac{A{{B}^{2}}+A{{C}^{2}}-B{{C}^{2}}}{2.AB.AC}$

Tương tự động tớ có: $\cos \widehat{ABC}=\frac{B{{A}^{2}}+B{{C}^{2}}-A{{C}^{2}}}{2.BA.BC}$ và $\cos \widehat{ACB}=\frac{C{{A}^{2}}+C{{B}^{2}}-A{{B}^{2}}}{2.CA.CB}$

Chú ý: $\overrightarrow{AB}.\overrightarrow{AC}=AB.AC\cos \widehat{BAC}=\frac{1}{2}\left( A{{B}^{2}}+A{{C}^{2}}-B{{C}^{2}} \right)$

■ Tính góc đằm thắm hai tuyến đường trực tiếp AB và CD tớ tính góc đằm thắm nhị vectơ $\overrightarrow{AB}$ và $\overrightarrow{CD}$ phụ thuộc vào công thức $\cos \left( \overrightarrow{AB};\overrightarrow{CD} \right)=\frac{\overrightarrow{AB}.\overrightarrow{CD}}{\left| \overrightarrow{AB} \right|.\left| \overrightarrow{CD} \right|}\Rightarrow \cos \left( AB;CD \right)=\frac{\left| \overrightarrow{AB}.\overrightarrow{CD} \right|}{\left| \overrightarrow{AB} \right|.\left| \overrightarrow{CD} \right|}$ kể từ cơ suy rời khỏi góc đằm thắm hai tuyến đường trực tiếp AB và CD.

Bài thói quen góc đằm thắm hai tuyến đường trực tiếp d1 và d2 bởi vì với đáp án chi tiết

Bài tập luyện 1: Cho hình chóp S.ABC với lòng là tam giác đều cạnh a, $SA\bot \left( ABC \right)$ và $SA=a\sqrt{3}$. Gọi M, N theo thứ tự là trung điểm của AB và SC. Tính cosin góc đằm thắm hai tuyến đường trực tiếp AN và CM.

Lời giải chi tiết

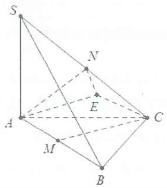
Cách 1: Dựng hình bình hành AMCE suy rời khỏi $AM=CE=\frac{a}{2}$.

Khi cơ $AE//CM\Rightarrow \left( \widehat{AE;CM} \right)=\left( \widehat{AN;AE} \right)=\varphi .$

Mặt không giống $SC=\sqrt{S{{A}^{2}}+A{{C}^{2}}}=2a\Rightarrow $ chừng nhiều năm đàng trung tuyến AN là $AN=\frac{SC}{2}=a.AE=CM=\frac{a\sqrt{3}}{2}.$

Do $\Delta ABC$ đều nên $CM\bot AM\Rightarrow $ AMCE là hình chữ nhật.

Khi cơ $CE\bot AE$ tuy nhiên $CE\bot SA\Rightarrow CE\bot \left( SAE \right)\Rightarrow CE\bot SE.$

$\Delta SEC$ vuông bên trên E với đàng trung tuyến $EN=\frac{1}{2}SC=a.$

Ta có: $\cos \widehat{NAE}=\frac{A{{N}^{2}}+A{{E}^{2}}-N{{E}^{2}}}{2.AN.AE}=\frac{\sqrt{3}}{4}>0\Rightarrow \cos \varphi =\frac{\sqrt{3}}{4}.$

Cách 2: Ta có: $\overrightarrow{AN}=\frac{1}{2}\left( \overrightarrow{AS}+\overrightarrow{AC} \right);\overrightarrow{CM}=\overrightarrow{AM}-\overrightarrow{AC}=\frac{1}{2}\overrightarrow{AB}-\overrightarrow{AC}.$

Khi cơ $\overrightarrow{AN}.\overrightarrow{CM}=\frac{1}{2}\left( \overrightarrow{AS}+\overrightarrow{AC} \right)\left( \frac{1}{2}\overrightarrow{AB}-\overrightarrow{AC} \right)=\frac{1}{4}\overrightarrow{AB}.\overrightarrow{AC}-\frac{1}{2}A{{C}^{2}}=\frac{1}{4}{{a}^{2}}\cos 60{}^\circ -\frac{{{a}^{2}}}{2}=\frac{-3{{a}^{2}}}{8}.$

Lại có: $AN=\frac{SC}{2}=a;CM=\frac{a\sqrt{3}}{2}\Rightarrow \cos \varphi =\frac{\left| \frac{-3{{a}^{2}}}{8} \right|}{a.\frac{a\sqrt{3}}{2}}=\frac{\sqrt{3}}{4}.$

Bình luận: Dựa vô nhị thủ tục bên trên tớ thấy rằng, vô một số trong những tình huống, việc dùng khí cụ vectơ nhằm tính góc đằm thắm hai tuyến đường trực tiếp chung câu hỏi trở thành dễ dàng ràng rộng lớn đặc biệt nhiều!.

Bài tập luyện 2: Cho hình chóp S.ABC với $SA=SB=SC=AB=a;AC=a\sqrt{2}$ và $BC=a\sqrt{3}$. Tính cosin góc đằm thắm hai tuyến đường trực tiếp SC và AB.

Lời giải chi tiết

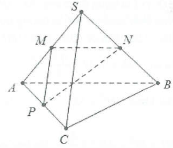
Cách 1: Gọi M, N, Phường theo thứ tự là trung điểm của SA, SB và AC. Khi cơ $\left\{ \begin{array}  {} MP//SC \\  {} N//AB \\ \end{array} \right.\Rightarrow \left( \widehat{SC;AB} \right)=\left( \widehat{MP;MN} \right).$

Ta có: $MN=\frac{AB}{2}=\frac{a}{2};MP=\frac{SC}{2}=\frac{a}{2}.$

Mặt không giống $\Delta SAC$ vuông bên trên S $\Rightarrow SP=\frac{AC}{2}=\frac{a\sqrt{2}}{2}.$

$B{{P}^{2}}=\frac{B{{A}^{2}}+B{{C}^{2}}}{2}-\frac{A{{C}^{2}}}{4}=\frac{3}{2}{{a}^{2}}\Rightarrow BP=\frac{a\sqrt{6}}{2}.$

Suy rời khỏi $P{{N}^{2}}=\frac{P{{S}^{2}}+P{{B}^{2}}}{2}-\frac{S{{B}^{2}}}{4}=\frac{3{{a}^{2}}}{4}\Rightarrow NP=\frac{a\sqrt{3}}{2}.$

Khi cơ $\cos \widehat{NMP}=\frac{M{{N}^{2}}+M{{P}^{2}}-N{{P}^{2}}}{2.MN.MP}=-\frac{1}{2}\Rightarrow \widehat{NMP}=120{}^\circ \Rightarrow \varphi =\left( \widehat{SC;AB} \right)=60{}^\circ .$

Cách 2: Ta có: $\overrightarrow{AB}=\overrightarrow{SB}-\overrightarrow{SA}\Rightarrow \overrightarrow{AB}.\overrightarrow{SC}=\left( \overrightarrow{SB}-\overrightarrow{SA} \right).\overrightarrow{SC}=\overrightarrow{SB}.\overrightarrow{SC}-\overrightarrow{SA}.\overrightarrow{SC}$

$=\frac{1}{2}\left( S{{B}^{2}}+S{{C}^{2}}-A{{C}^{2}} \right)-\frac{1}{2}\left( S{{A}^{2}}+S{{C}^{2}}-A{{B}^{2}} \right)=-\frac{{{a}^{2}}}{2}.$

Suy rời khỏi $\cos \left( SC;AB \right)=\frac{\left| \frac{-{{a}^{2}}}{2} \right|}{a.a}=\frac{1}{2}\Rightarrow \left( SC;AB \right)=60{}^\circ .$

Bài tập luyện 3: Cho tứ diện ABCD với $AB={{x}_{1}},CD={{x}_{2}};AC={{y}_{1}},BD={{y}_{2}},BC={{z}_{1}},AD={{z}_{2}}$. Tính góc đằm thắm hai tuyến đường trực tiếp BC và AD.

Lời giải chi tiết

Ta có: $\overrightarrow{BC}.\overrightarrow{DA}\text{ }=\text{ }\overrightarrow{BC}\left( \overrightarrow{DC}+\overrightarrow{CD} \right)=\overrightarrow{CB}.\overrightarrow{CD}-\overrightarrow{CB}.\overrightarrow{CD}$

$=\frac{1}{2}\left( C{{B}^{2}}+C{{D}^{2}}-B{{D}^{2}} \right)-\frac{1}{2}\left( C{{B}^{2}}+C{{A}^{2}}-A{{B}^{2}} \right)=\frac{1}{2}\left( A{{B}^{2}}+C{{D}^{2}}-B{{D}^{2}}-C{{A}^{2}} \right).$

Khi cơ $\cos \left( BC;DA \right)=\frac{\left| \overrightarrow{BC}.\overrightarrow{DA} \right|}{BC.DA}=\frac{x_{1}^{2}+x_{2}^{2}+y_{1}^{2}-y_{2}^{2}}{2{{z}_{1}}{{z}_{2}}}.$

Đặc biệt: Nếu $AB=CD=x;AC=BD=y$ và $BC=AD=z$ tớ bịa $\left\{ \begin{array}  {} \alpha =\left( \widehat{BC;AD} \right) \\  {} \beta =\left( \widehat{AB;CD} \right) \\  {} \gamma =\left( \widehat{AC;BD} \right) \\ \end{array} \right.$ thì tớ có:

$\cos \alpha =\frac{{{x}^{2}}-{{y}^{2}}}{{{z}^{2}}};\cos \beta =\frac{\left| {{y}^{2}}-{{z}^{2}} \right|}{{{x}^{2}}};\cos \gamma =\frac{{{z}^{2}}-{{z}^{2}}}{{{y}^{2}}}.$

Bài tập luyện 4: Cho hình chóp S.ABCD với lòng là hình vuông vắn ABCD cạnh 2a, $SA\bot \left( ABCD \right)$ và $SB=a\sqrt{5}$. Gọi M là trung điểm của AB và N là trung điểm của BC. Tính cosin góc đằm thắm 2 đường thẳng liền mạch SM và Doanh Nghiệp .

Lời giải chi tiết

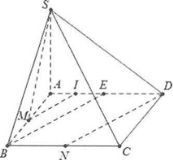
■ Cách 1: Do $SA\bot \left( ABCD \right).$

Ta có: $SA=\sqrt{S{{B}^{2}}-A{{B}^{2}}}=a$. Gọi E là trung điểm của AD và I là trung điểm của AE. Dễ thấy BNDE là hình bình hành và XiaoMI là đàng khoảng vô tam giác ABE. Khi cơ $DN//BE//MI.$

Tacó: $AM=a;AI=\frac{AE}{2}=\frac{a}{2}.$

Mặt khác: $S{{M}^{2}}=S{{A}^{2}}+A{{M}^{2}}=2{{a}^{2}};S{{I}^{2}}=\frac{5{{a}^{2}}}{4}.$

$MI=A{{I}^{2}}+A{{M}^{2}}=\frac{5{{a}^{2}}}{4}$. Do vậy $\cos \widehat{SMI}=\frac{S{{M}^{2}}+M{{I}^{2}}-S{{I}^{2}}}{2.SM.MI}=\frac{\sqrt{10}}{5}=cos(\widehat{SM;DN}).$

■ Cách 2: Ta có: $\overrightarrow{SM}.\overrightarrow{DN}\text{ }=\text{ }\overrightarrow{SM}.\left( \overrightarrow{SN}-\overrightarrow{SD} \right)=\overrightarrow{SM}.\overrightarrow{SN}\text{ }-\text{ }\overrightarrow{SM}.\overrightarrow{SD}$

$\text{=}\frac{1}{2}\left( S{{M}^{2}}+S{{N}^{2}}-M{{N}^{2}} \right)-\frac{1}{2}\left( S{{M}^{2}}+S{{D}^{2}}-M{{D}^{2}} \right)$

Mặt khác: $S{{N}^{2}}=S{{A}^{2}}+A{{N}^{2}}=S{{A}^{2}}+A{{B}^{2}}+B{{N}^{2}}=6{{a}^{2}},MN=\frac{AC}{2}=\text{ }a\sqrt{2},S{{D}^{2}}=5{{a}^{2}},M{{D}^{2}}=5{{a}^{2}}.$

Do cơ $\overrightarrow{SM}.\overrightarrow{DN}=2{{a}^{2}}\Rightarrow \cos \left( SM;DN \right)=\frac{\left| 2{{a}^{2}} \right|}{SM.DN}=\frac{2{{a}^{2}}}{a\sqrt{2}.a\sqrt{5}}=\frac{\sqrt{10}}{5}.$

Lời giải chi tiết

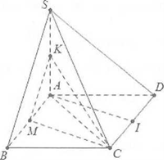
a) Do $BC//AD\Rightarrow (\widehat{SD;BC})=(\widehat{SD;AD})=\widehat{SDA}$

$\Delta SAD$ vuông bên trên A $\Rightarrow \cos \widehat{SDA}=\frac{AD}{SD}=\frac{AD}{\sqrt{A{{D}^{2}}+S{{A}^{2}}}}=\frac{1}{\sqrt{3}}.$

Xem thêm: 30 Hình Ảnh Phật Thích Ca Mâu Ni - Tương Truyền Và Biểu Tượng Soi Sáng

b) Gọi M, K theo thứ tự là trung điểm của AB và SA thì MK là đàng khoảng vô tam giác SAB.

Khi cơ $MK//SB$, mặt mày không giống $MC//AI.$

Suy rời khỏi $(\widehat{SB;AI})=(\widehat{MK;CM}).$

Ta có: $MK=\frac{SB}{2}=\frac{\sqrt{S{{A}^{2}}+A{{B}^{2}}}}{2}=\frac{a\sqrt{5}}{2}$; $MC=\sqrt{M{{B}^{2}}+B{{C}^{2}}}=\frac{3a}{2}$; $KC=\sqrt{K{{A}^{2}}+A{{C}^{2}}}=2a.$

Khi cơ $cos\widehat{KMC}=\frac{K{{M}^{2}}\text{+ }M{{C}^{2}}-K{{C}^{2}}}{2.KM.MC}=-\frac{1}{3\sqrt{5}}\Rightarrow cos\left( \widehat{SB;AI} \right)=\frac{1}{3\sqrt{5}}.$

Cách khác: Ta có:$\overrightarrow{SB}.\overrightarrow{AI}=\overrightarrow{SB}.\left( \overrightarrow{SI}-\overrightarrow{SA} \right)=\overrightarrow{SB}.\overrightarrow{SI}-\overrightarrow{SB}.\overrightarrow{SA}$

$=\frac{1}{2}\left( S{{B}^{2}}+S{{I}^{2}}-I{{B}^{2}} \right)-\frac{1}{2}\left( S{{B}^{2}}+S{{A}^{2}}-A{{B}^{2}} \right)$

Do $S{{B}^{2}}=5{{a}^{2}};S{{I}^{2}}=S{{A}^{2}}+A{{D}^{2}}+D{{I}^{2}}=\frac{25{{a}^{2}}}{4};AI=\sqrt{A{{D}^{2}}+D{{I}^{2}}}=\frac{3a}{2}=IB.$

Suy rời khỏi $\overrightarrow{SB}.\overrightarrow{AI}=\frac{{{a}^{2}}}{2}\Rightarrow \cos \left( SB;AI \right)=\frac{\left| \overrightarrow{SB}.\overrightarrow{AI} \right|}{SB.AI}=\frac{\frac{{{a}^{2}}}{2}}{a\sqrt{5}.\frac{3a}{2}}=\frac{1}{3\sqrt{5}}.$

Lời giải chi tiết

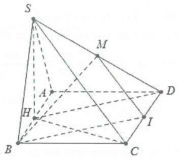
a) Do $AB=BC=a$, $\widehat{ABC}=60{}^\circ \Rightarrow \Delta ABC$ đều cạnh a.

Gọi H là trung điểm của AB, bởi tam giác SAB cân nặng bên trên S nên $SH\bot AB.$

Mặt không giống $\left\{ \begin{array}  {} \left( SAB \right)\bot \left( ABCD \right) \\  {} AB=\left( SAB \right)\cap \left( ABCD \right) \\ \end{array} \right.\Rightarrow SH\bot \left( ABC \right).$

$\Delta ABC$ đều nên $CH=\frac{a\sqrt{3}}{2},\left( \widehat{SC;\left( ABC \right)} \right)=\text{ }\widehat{SCH}=30{}^\circ $

Ta có: $SH=HC\tan 30{}^\circ =\frac{a}{2}.$

Do $\widehat{ABC}=60{}^\circ \Rightarrow \widehat{BAD}=120{}^\circ \Rightarrow HD=\sqrt{A{{H}^{2}}+A{{D}^{2}}-2AH.AD\cos 120{}^\circ }=\frac{a\sqrt{7}}{2}.$

Suy rời khỏi $SA=\sqrt{S{{H}^{2}}+H{{A}^{2}}}=\frac{a\sqrt{2}}{2}$, $SD=\sqrt{S{{H}^{2}}+H{{D}^{2}}}=a\sqrt{2}$.

Mặt không giống $AD//BC\text{ }\Rightarrow \left( \widehat{BC;SD} \right)=\left( \widehat{AD;SD} \right)$, $\cos \widehat{SDA}=\frac{D{{S}^{2}}+D{{A}^{2}}-S{{A}^{2}}}{2.DS.DA}=\frac{5\sqrt{2}}{8}.$

Do vậy $cos\left( \widehat{BC;SD} \right)=\frac{5\sqrt{2}}{8}.$

b) Ta với $\overrightarrow{SC}.\overrightarrow{DH}=\overrightarrow{SC}.\left( \overrightarrow{SH}-\overrightarrow{SD} \right)=\text{ }\overrightarrow{SC}.\overrightarrow{SH}-\overrightarrow{SC}.\overrightarrow{SD}$

$=\frac{1}{2}\left( S{{H}^{2}}+S{{C}^{2}}-H{{C}^{2}} \right)-\frac{1}{2}\left( S{{C}^{2}}+S{{D}^{2}}-C{{D}^{2}} \right)=-\frac{3{{a}^{2}}}{4}$

Mặt khác: $SC=\sqrt{S{{H}^{2}}+H{{C}^{2}}}=a\Rightarrow \cos \left( SC;DH \right)=\frac{\left| \overrightarrow{SC};\overrightarrow{DH} \right|}{SC.DH}=\frac{\frac{3{{a}^{2}}}{4}}{a.\frac{a\sqrt{7}}{2}}=\frac{3\sqrt{7}}{14}.$

Cách khác: Gọi I là trung điểm của CD$\Rightarrow \left\{ \begin{array}  {} DH//BI \\  {} DH=BI=\frac{a\sqrt{7}}{2} \\ \end{array} \right.$, gọi M là trung điểm của SD

$\Rightarrow \left\{ \begin{array}  {} MI//SC \\  {} MI=\frac{SC}{2}=\frac{a}{2} \\ \end{array} \right.$. Lại có: $BD=a\sqrt{3}$; $SB=\sqrt{S{{H}^{2}}+H{{B}^{2}}}=\frac{a\sqrt{2}}{2}.$

Do cơ $B{{M}^{2}}=\frac{B{{D}^{2}}+B{{S}^{2}}}{2}-\frac{S{{D}^{2}}}{4}=\frac{5{{a}^{2}}}{4}\Rightarrow \cos \widehat{MIB}=\frac{M{{I}^{2}}+I{{B}^{2}}-M{{B}^{2}}}{2.IM.IB}=\frac{3\sqrt{17}}{14}.$

Suy rời khỏi $\cos \left( \widehat{DH;SC} \right)=\frac{3\sqrt{17}}{14}.$

Lời giải chi tiết

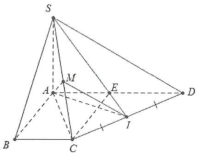
a) Ta có: $AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=a\sqrt{2}.$

Do $SA\bot \left( ABCD \right)\Rightarrow \left( \widehat{SC;\left( ABC \right)} \right)=\widehat{SCA}=\text{ }60{}^\circ .$

Khi cơ $SA=AC\tan 60{}^\circ =a\sqrt{6}.$

Do $AD//BC\Rightarrow \left( \widehat{BC;SD} \right)=\left( \widehat{AD;SD} \right).$

Mặt không giống $\cos \widehat{ADS}=\frac{AD}{SD}~~=\frac{AD}{\sqrt{S{{A}^{2}}+A{{D}^{2}}}}~$

$=\frac{2a}{\sqrt{6{{a}^{2}}+4{{a}^{2}}}}~=\frac{\sqrt{10}}{5}=c\text{os}\widehat{\left( \text{BC;SD} \right)}.$

b) Gọi E là trung điểm của $AD\Rightarrow AE=DE=BC=a\Rightarrow $ ABCE là hình vuông vắn cạnh a.

Do $CE=\frac{1}{2}AD\Rightarrow \Delta ACD$ vuông bên trên C.

Ta có: $CD=\sqrt{C{{E}^{2}}+E{{D}^{2}}}=a\sqrt{2}\Rightarrow ID=\frac{a\sqrt{2}}{2}.$

Lại có: $\overrightarrow{AI}.\overrightarrow{SD}=\left( \overrightarrow{SI}-\overrightarrow{SA} \right).\overrightarrow{SD}=\overrightarrow{SI}.\overrightarrow{SD}-\overrightarrow{SA}.\overrightarrow{SD}=\frac{1}{2}\left( S{{I}^{2}}+S{{D}^{2}}-D{{I}^{2}} \right)-\frac{1}{2}\left( S{{A}^{2}}+S{{D}^{2}}-A{{D}^{2}} \right)$

Trong cơ $A{{I}^{2}}=A{{C}^{2}}+C{{I}^{2}}=\frac{5{{a}^{2}}}{2}\Rightarrow S{{I}^{2}}=S{{A}^{2}}+A{{I}^{2}}=\frac{17{{a}^{2}}}{2}.$

Do cơ $\overrightarrow{AI}.\overrightarrow{SD}=3{{a}^{2}}\Rightarrow \cos \left( AI;SD \right)=\frac{3{{a}^{2}}}{AI.SD}=\frac{3{{a}^{2}}}{a\sqrt{10}}=\frac{3}{5}.$

Cách khác: Gọi M là trung điểm của SC$\Rightarrow \left\{ \begin{array}  {} MI//SD \\  {} MI=\frac{SD}{2}=\frac{a\sqrt{10}}{2} \\ \end{array} \right.,AI=\frac{a\sqrt{10}}{2},AM=\frac{SC}{2}=a\sqrt{2}.$

Khi cơ $\widehat{MIA}=\frac{I{{M}^{2}}+I{{A}^{2}}-A{{M}^{2}}}{2.IM.IA}=\frac{3}{5}.$

Lời giải chi tiết

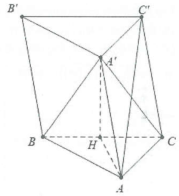
a) Gọi H là trung điểm của BC.

Ta có: $BC//{B}'{C}'\Rightarrow \left( \widehat{{B}'{C}';{A}'C} \right)=\left( \widehat{BC;{A}'C} \right)=\widehat{{A}'CH}.$

Mặt không giống ${A}'H\bot \left( ABC \right)\Rightarrow \left( \widehat{A{A}';\left( ABC \right)} \right)=\widehat{A{A}'H}=60{}^\circ .$

$AH=\frac{a\sqrt{3}}{2}\Rightarrow {A}'H=AH\tan 60{}^\circ =\frac{3a}{2}.$

Xét tam giác vuông ${A}'HC$ tớ có: $\tan \widehat{{A}'CH}=\frac{{A}'H}{HC}=3.$

Vậy $\left( \widehat{B{C}';{A}'C} \right)=3.$

b) Do $C{C}'//A{A}'\Rightarrow \widehat{\left( C{C}';AB \right)}=\widehat{\left( A{A}';AB \right)}$

Xem thêm: 999+ Ảnh FF Đẹp Nhất, Hình Nền Free Fire Cực Ngầu

Ta có: ${A}'A=\sqrt{A{{H}^{2}}+H{{A}^{2}}}=a\sqrt{3}.$

${A}'B=\sqrt{{A}'{{H}^{2}}+H{{B}^{2}}}=\frac{a\sqrt{10}}{2}\Rightarrow \cos \widehat{{A}'AB}=\frac{A{{{{A}'}}^{2}}+A{{B}^{2}}-{A}'{{B}^{2}}}{2.A{A}'.AB}=\frac{\sqrt{3}}{4}.$

Vậy $\cos \left( C{C}';AB \right)=\frac{\sqrt{3}}{4}.$