Để tính khoảng cách thân thiết hai tuyến phố trực tiếp chéo cánh nhau tớ rất có thể sử dụng một trong số cơ hội sau:
* Phương pháp 1
Chọn mặt mày phẳng phiu (α) chứa chấp đường thẳng liền mạch Δ và tuy nhiên song với Δ'. Khi bại d(Δ, Δ') = d(Δ', (α))
Bạn đang xem: Cộng đồng hỏi đáp - giainhanh.vn
* Phương pháp 2
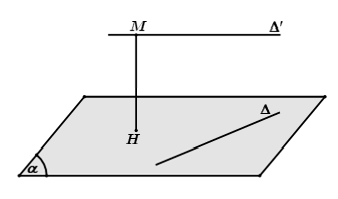
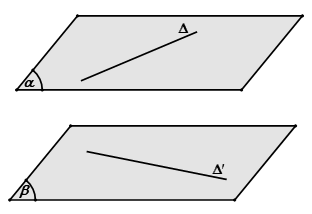
Dựng nhì mặt mày phẳng phiu tuy nhiên song và thứu tự chứa chấp hai tuyến phố trực tiếp. Khoảng cơ hội thân thiết nhì mặt mày phẳng phiu này là khoảng cách cần thiết dò thám.
Ví dụ 1:
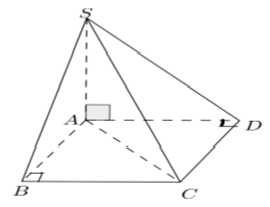
Cho hình chóp S.ABCD với SA ⊥ (ABCD), lòng ABCD là hình chữ nhật với AC = a√5 và BC = a√2. Tính khoảng cách thân thiết SD và BC.
Hướng dẫn giải

 Chọn D
Chọn D
Ta có: BC // AD (Tính hóa học hình chữ nhật) nhưng mà AD ⊂ (SAD)
⇒ BC // mp(SAD)
d(BC, SD) = d(BC, (SAD)) = d(B, SAD)
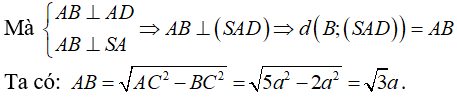 Vậy d(SD; BC) = AB = a√3
Vậy d(SD; BC) = AB = a√3
Ví dụ 2:
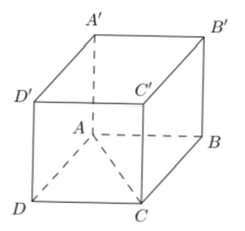
Cho hình lập phương ABCD.A'B'C'D' với cạnh bởi vì a. Khoảng cơ hội thân thiết BB’ và AC bằng:
Hướng dẫn giải

 Chọn C.
Chọn C.
+ Ta có: BB’ // CC’ nhưng mà CC’ ⊂ (ACC’A’) nên: BB’ // (ACC’A’)
⇒ d( BB’; AC) = d( BB’; (ACC’A’) = d(B; (ACC’A’)
+ Gọi O là gửi gắm điểm của AC và BD
⇒ BO ⊥ (ACC’A’) ( đặc điểm hình lập phương )
Ví dụ 3:
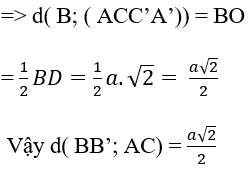 Cho hình chóp S.ABCD với lòng là hình thang vuông bên trên A và B; AB = BC = a và AD = 2a; SA vuông góc với mặt mày lòng và SA = a. Tính khoảng cách thân thiết SB và CD?
Cho hình chóp S.ABCD với lòng là hình thang vuông bên trên A và B; AB = BC = a và AD = 2a; SA vuông góc với mặt mày lòng và SA = a. Tính khoảng cách thân thiết SB và CD?
Hướng dẫn giải

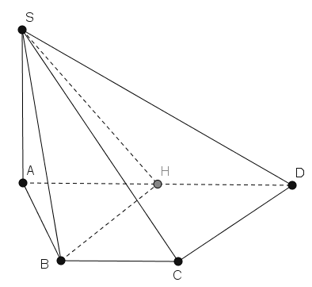 Gọi H là trung điểm AD suy rời khỏi : AH = HD = a
Gọi H là trung điểm AD suy rời khỏi : AH = HD = a
+ Tứ giác HDCB với HD // BC và HD = BC = a
⇒ HDCB là hình bình hành.
⇒ CD // HB nên CD // mp(SHB)
+ Do H là trung điểm của AB và CD // (SHB) nên: d(CD; SB) = d(CD ;(SBH))= d(D; (SBH)) = d(A ;(SBH))
+ Tứ diện A. BHS với :
AB = AH = AS và AB ; AH ; SA song một vuông góc nên:
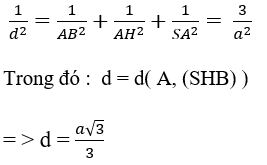 Vậy d(SB ; CD) = d( A, (SHB)) = (a√3)/3
Vậy d(SB ; CD) = d( A, (SHB)) = (a√3)/3
Chọn đáp án C
Ví dụ 4:
Cho hình chóp S.ABCD với lòng là hình vuông vắn cạnh a. Đường trực tiếp SA vuông góc với mặt mày phẳng phiu lòng, SA = a. Khoảng cơ hội thân thiết hai tuyến phố trực tiếp SB và CD nhận độ quý hiếm này trong số độ quý hiếm sau?
A. a B. a√2 C. a√3 D. 2a
Hướng dẫn giải
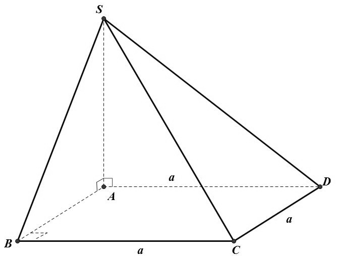 Ta có: CD // AB nên CD // (SAB)
Ta có: CD // AB nên CD // (SAB)
⇒ d(CD; AB) = d(CD; (SAB)) = d(D; SAB)) = AD = a
(vì AD ⊥ AB và AD ⊥ SA nên AD ⊥ (SAB))
Chọn phương án A
Ví dụ 5:
Cho tứ diện OABC vô bại OA; OB; OC song một vuông góc cùng nhau và OA = OB = OC = a. Gọi I là trung điểm BC. Khoảng cơ hội thân thiết AI và OC bởi vì bao nhiêu?
Hướng dẫn giải

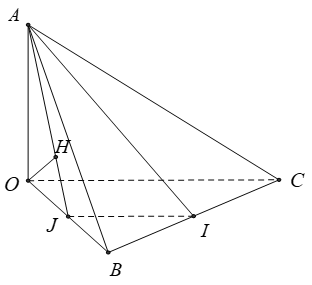 Gọi J là trung điểm OB. Kẻ OH vuông góc AJ bên trên H
Gọi J là trung điểm OB. Kẻ OH vuông góc AJ bên trên H
+ Tam giác AOJ vuông bên trên O , với OH là đàng cao
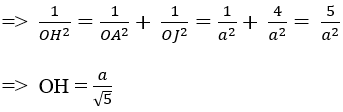 + Do I và J thứu tự là trung điểm của BC và BO nên IJ là đàng khoảng của tam giác ABC và IJ // OC
+ Do I và J thứu tự là trung điểm của BC và BO nên IJ là đàng khoảng của tam giác ABC và IJ // OC
Mà IJ ⊂ (AIJ) nên OC // (AIJ) .
+ Ta với 3 đường thẳng liền mạch OA; OB; OC song một vuông góc nên OC ⊥ (OAB)
⇒ IJ ⊥ (OAB) và IJ ⊥ OH (1)
Lại có: AJ ⊥ OH (2)
Từ ( 1) và (2) suy ra: OH ⊥ (AIJ)
+ Khi đó; d(AI; OC) = d(OC; (AIJ)) = d(O; (AIJ)) = OH = a/√5
Chọn đáp án B
Ví dụ 6:
Cho hình vuông vắn ABCD và tam giác đều SAD trực thuộc nhì mặt mày phẳng phiu vuông góc cùng nhau và AD = a. Tính khoảng cách thân thiết AD và SB
Hướng dẫn giải
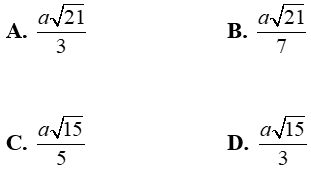
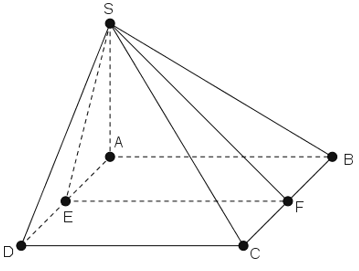 Gọi E, F thứu tự là trung điểm AD và B.
Gọi E, F thứu tự là trung điểm AD và B.
+ Tam giác SAD là tam giác đều nên SE ⊥ AD (1)
+ Lại có; nhì mp(ABCD) và (SAD) rời nhau bám theo gửi gắm tuyến AD và trực thuộc nhì mặt mày phẳng phiu vuông góc cùng nhau (2) .
Từ (1) và (2) suy ra: SE ⊥ (ABCD) .
+ Gọi H là hình chiếu vuông góc của E lên SF. Ta minh chứng EH ⊥ (SBC).
Thật vậy, tớ có: EH ⊥ SF ( cơ hội dựng) và EH ⊥ BC (do BC ⊥ (SEF)
⇒ EH ⊥ (SBC) .
+ Do AD // BC; SB ⊂ (SBC) và EH ⊥ (SBC)
⇒ d(AD: SB) = d(AD; (SBC) = d(E; (SBC)) = EH
+ Xét tam giác vuông SEF có:
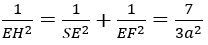 trong đó: SE = a√3; EF = AB = a
trong đó: SE = a√3; EF = AB = a
⇒ EH = (a√21)/7
Chọn đáp án B
Ví dụ 7:
Cho hình lập phương ABCD.A'B'C'D' với cạnh bởi vì a. Khoảng cơ hội thân thiết BB’ và AC bằng
Hướng dẫn giải

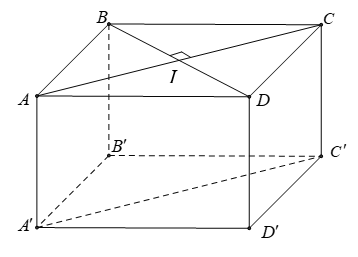
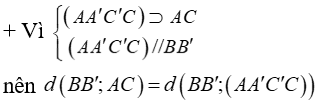
Gọi I là gửi gắm điểm của AC và BD.
+ Vì ABCD.A’B’C’D’ là hình lập phương nên BI ⊥ (AA'C'C).
+ Ta có: BD = BC√2 = a√2 nên IB = BD/2 = (a√2)/2
+ Lúc đó:
d(BB’; AC)= d(BB’;( AA’C’C) = IB = (a√2)/2
Chọn đáp án C
Ví dụ 8:
Cho hình chóp S.ABC với lòng ABC là tam giác vuông bên trên B; AB = a cạnh mặt mày SA vuông góc với lòng và SA = a√2. Gọi M là trung điểm của AB. Khoảng cơ hội thân thiết SM và BC bởi vì bao nhiêu?
Hướng dẫn giải
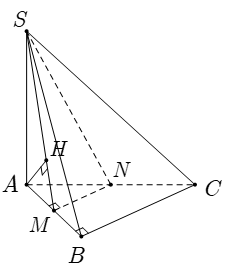 Gọi N là trung điểm của cạnh lòng AC.
Gọi N là trung điểm của cạnh lòng AC.
+ Tam giác ABC với MN là đàng khoảng nên MN // BC
⇒ BC // ( SMN) nhưng mà SM ⊂ (SMN) nên :
d(SM; BC) = d(BC; (SMN)) = d(B; (SMN)) = d(A; (SMN))
Gọi H là hình chiếu vuông góc của A bên trên đoạn SM.
+ Ta hội chứng minh: MN ⊥ (SAM):
 Chọn đáp án A
Chọn đáp án A
Ví dụ 9:
Cho lăng trụ tam giác đều ABC. 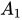
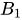
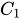 với cạnh lòng bởi vì a, cạnh mặt mày bởi vì b Tính khoảng cách thân thiết AB và
với cạnh lòng bởi vì a, cạnh mặt mày bởi vì b Tính khoảng cách thân thiết AB và 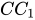
Hướng dẫn giải
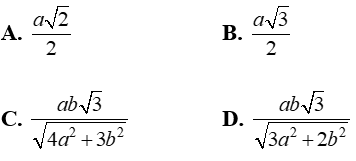
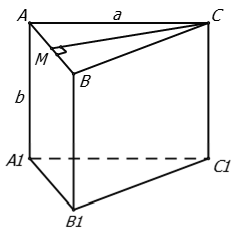 Gọi M là trung điểm của AB
Gọi M là trung điểm của AB
+ Ta có: 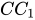 //
// 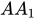 nhưng mà
nhưng mà 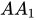 ⊂ (
⊂ ( 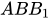
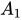 )
)
⇒ 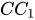 // (
// ( 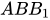
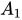 )
)
⇒ d(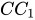 ; AB) = d(
; AB) = d(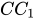 ; (
; (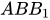
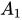 )) = d(C; (
)) = d(C; ( 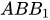
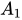 ))
))
+ Ta minh chứng CM ⊥ (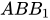
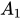 ):
):
- Do tam giác ABC đều nên CM là đàng trung tuyến mặt khác là đàng cao: CM ⊥ AB. (1)
- CM ⊥ 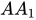 ( đặc điểm lăng trụ tam giác đều) (2)
( đặc điểm lăng trụ tam giác đều) (2)
Mà AB và 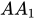 (
(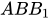
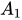 ), kết phù hợp với (1) và (2) suy ra:
), kết phù hợp với (1) và (2) suy ra:
CM ⊥ (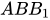
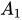 )
)
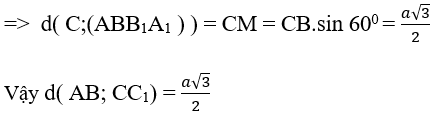 Đáp án B
Đáp án B
Ví dụ 10:
Cho hình chóp S.ABCD với lòng là hình vuông vắn cạnh a, SD = a√17/2. Hình chiếu vuông góc H của đỉnh S lên trên bề mặt phẳng phiu (ABCD) là trung điểm của cạnh AB. Gọi K là trung điểm của AD. Tính khoảng cách thân thiết hai tuyến phố SD và HK bám theo a
Hướng dẫn giải
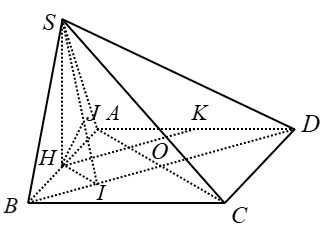 + Ta có: H và K thứu tự là trung điểm của AB và AD nên HK là đàng khoảng của tam giác ABD
+ Ta có: H và K thứu tự là trung điểm của AB và AD nên HK là đàng khoảng của tam giác ABD
⇒ HK // BD ⇒ HK // (SBD)
⇒ d(SD; HK) = d(HK; (SBD)) = d(H, (SBD))
Kẻ HI ⊥ BD và HJ ⊥ SI
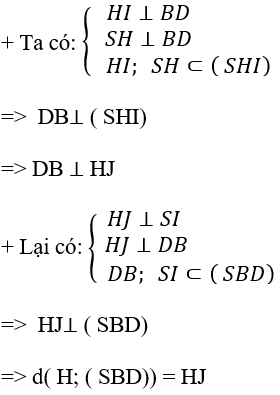
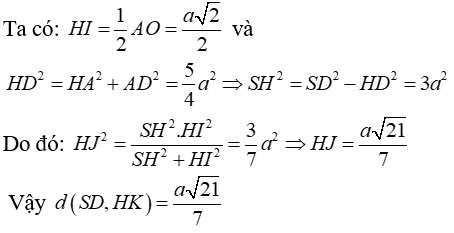
Chọn đáp án C
Ví dụ 11:
Cho hình chóp tứ giác S.ABCD với lòng ABCD là hình vuông vắn tâm O, cạnh bởi vì 2a. Mặt mặt mày SAB là tam giác đều, SI vuông góc với (SCD) và I là trung điểm AB. Khoảng cơ hội thân thiết hai tuyến phố trực tiếp SO và AB là:
Hướng dẫn giải
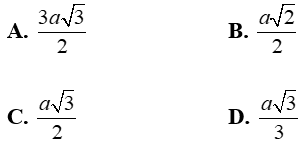
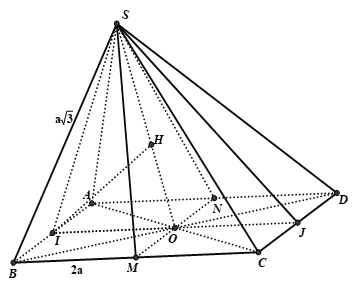 Kẻ MN // AB ⇒ AB // (SMN)
Kẻ MN // AB ⇒ AB // (SMN)
⇒ d(SO; AB) = d(AB; (SMN)) = d(I, (SMN))
Ta có: AB ⊥ SI ⇒ MN ⊥ SI, AB ⊥ OI ⇒ MN ⊥ OI
⇒ MN ⊥ (SOI) ⇒ (SMN) ⊥ (SOI).
Kẻ IH ⊥ SO ⇒ IH ⊥ (SMN)
⇒ IH = d(I, (SMN))
+ Gọi J là trung điểm của CD
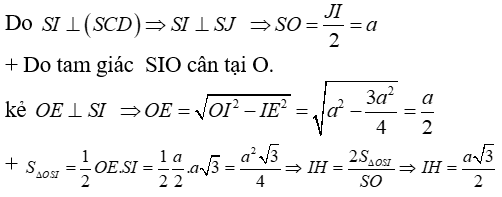 Chọn C
Chọn C
Ví dụ 12:
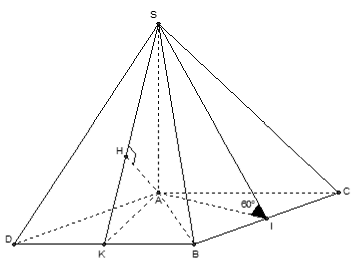
Cho hình chóp S. ABC với lòng là tam giác ABC vuông bên trên C, AB = 5a, BC = 4a Cạnh SA vuông góc với lòng và góc thân thiết mặt mày phẳng phiu (SBC) với mặt mày lòng (ABC) bởi vì 60° Gọi D là trung điểm của cạnh AB. Khoảng cơ hội thân thiết hai tuyến phố trực tiếp SD và BC là:
Hướng dẫn giải
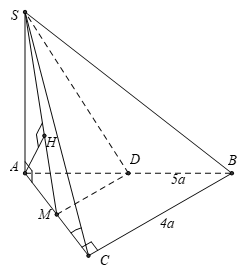 + Gọi M là trung điểm AC , tớ với DM là đàng khoảng của tam giác ABC nên DM // BC
+ Gọi M là trung điểm AC , tớ với DM là đàng khoảng của tam giác ABC nên DM // BC
⇒ BC // (SMD) .
⇒ d(BC; SD) = d(C; (SMD)) = d(A; (SMD))
Xem thêm: Giáp Tý 1984 mệnh gì? Nữ 1984 hợp hướng nào làm việc
+ Kẻ AH ⊥ SM (H ∈ SM), tớ có
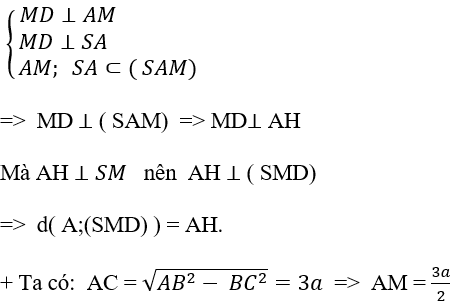 Do góc thân thiết mặt mày phẳng phiu (SBC) với mặt mày lòng (ABC) bởi vì 60° suy ra: ∠SCA = 60°.
Do góc thân thiết mặt mày phẳng phiu (SBC) với mặt mày lòng (ABC) bởi vì 60° suy ra: ∠SCA = 60°.
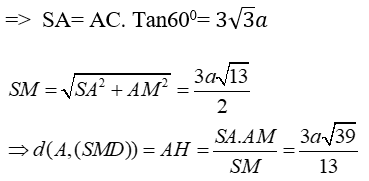 Chọn A
Chọn A
Câu 1:
Cho hình chóp S.ABCD với lòng ABCD là hình chữ nhật và AB = 2a; BC = a . Các cạnh mặt mày của hình chóp đều nhau và bởi vì a√2. Gọi E và F thứu tự là trung điểm của AB và CD; K là vấn đề ngẫu nhiên bên trên BC. Khoảng cơ hội thân thiết hai tuyến phố trực tiếp EF và SK là:
Hiển thị điều giải
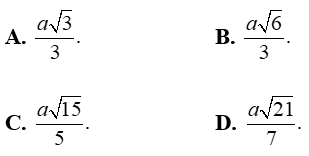
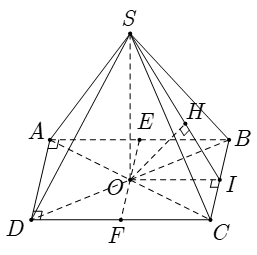 Gọi O là gửi gắm điểm của AC và BD; I là trung điểm cạnh BC
Gọi O là gửi gắm điểm của AC và BD; I là trung điểm cạnh BC
+ Do SA = SB = SC = SD và OA = OB = OC = OD nên SO ⊥ (ABCD)
+ Ta minh chứng BC ⊥ (SOI)
- Tam giác SBC cân nặng bên trên S với SI là đàng trung tuyến nên mặt khác là đàng cao : BC ⊥ SI (1).
- Lại có: BC ⊥ SO (vì SO ⊥ (ABCD)) (2)
Từ (1) và (2) suy ra: BC ⊥ (SOI)
Mà OH ⊂ (SOI) nên BC ⊥ OH
⇒ OH ⊥ (SBC)
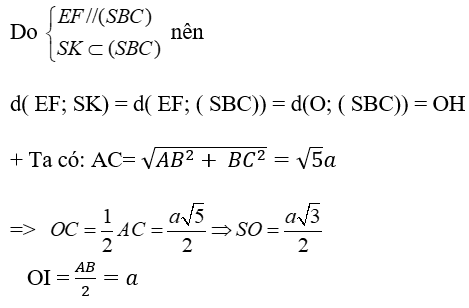 Xét tam giác SOI có:
Xét tam giác SOI có:
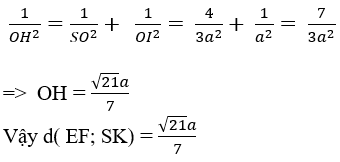 Chọn đáp án D
Chọn đáp án D
Câu 2:
Cho hình lập phương ABCD.A’B’C’D’ với cạnh bởi vì 1 (đvd). Khoảng cơ hội giữaAA’ và BD’ bằng:
Hiển thị điều giải
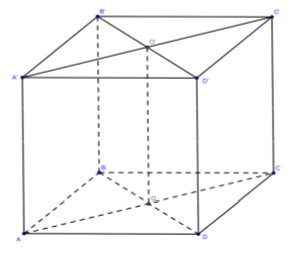 Ta có: AA’ // DD’ (tính hóa học hình lập phương)
Ta có: AA’ // DD’ (tính hóa học hình lập phương)
Mà DD ⊂ (BDD’B’)
⇒ AA’ // (BDD’B’)
⇒ d(AA’; BD’) = d(AA’; (BDD’B’)) = d(A; BDD’B’)
Gọi O là trung điểm của BD
⇒ AO ⊥ BD (tính hóa học hình vuông)
Lại có: AO ⊥ BB’
⇒ AO ⊥ (BDD’B’)
⇒ d(A; (BDD’B’) ) = AO
+ Xét tam giác ABD có:
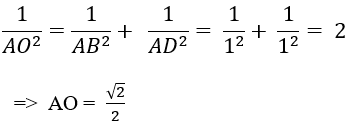 Chọn D
Chọn D
Câu 3:
Cho hình chóp S.ABCD với lòng ABCD là hình chữ nhật, BC = a√3; AB = a. Hai mặt mày phẳng phiu (SAC) và (SBD) nằm trong vuông góc với mặt mày lòng và đường thẳng liền mạch SC tạo ra với mặt mày lòng một góc 60°. Khoảng cơ hội thân thiết hai tuyến phố trực tiếp SB và AC.
Hiển thị điều giải
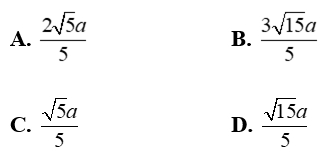
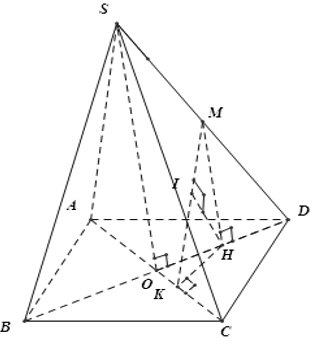 Chọn D
Chọn D
Gọi O là gửi gắm điểm của AC và BD
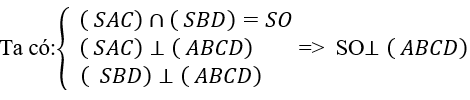
+ Do OC là hình chiếu vuông góc của SC bên trên mặt mày phẳng phiu (ABCD) ⇒ (SC, (ABCD)) = ∠SCO = 60°
+ Gọi M là trung điểm của SD. Khi đó; MO là đàng khoảng của tam giác SBD nên MO // SB
⇒ SB // (ACM).
+ Trong mặt mày phẳng phiu (SBD) kẻ MH // SO
⇒ MH ⊥ (ABCD)
Khi bại
d(SB; AC) = d(SB; (ACM)) = d(B; (ACM)) = 2d(H; (ACM))
+ Ta có: khoảng cách kể từ D cho tới AC là d:
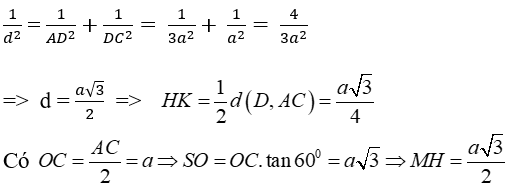 Xét tam giác vuông MHK đàng cao XiaoMi MI có:
Xét tam giác vuông MHK đàng cao XiaoMi MI có:
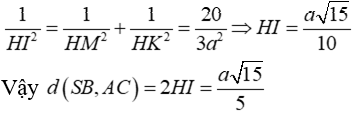
Câu 4:
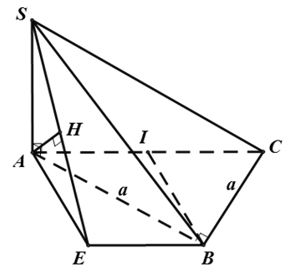
Cho hình chóp S. ABC với lòng ABC là tam giác vuông cân nặng bên trên B; AB = BC = a, SA vuông góc với mặt mày phẳng phiu (ABC) góc thân thiết đường thẳng liền mạch SC và mặt mày phẳng phiu (ABC) bởi vì 60°. Khoảng cơ hội thân thiết hai tuyến phố trực tiếp SB và AC.
Hiển thị điều giải
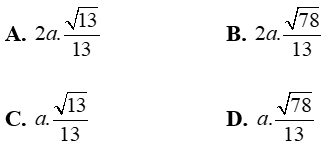
 Chọn D
Chọn D
+ Gọi I là trung điểm của AC .Qua B kẻ đường thẳng liền mạch d tuy nhiên song với AC.
Trong mặt mày phẳng phiu ( ABC) kẻ AE vuông góc với d bên trên E.
Khi bại AE ⊥ BE và AE ⊥ AC
+ Ta có: AC // BE nên AC // (SBE)
⇒ d (AC, SB) = d(A, (SBE)).
+ Gọi AH là đàng cao của (SAE) , tớ có
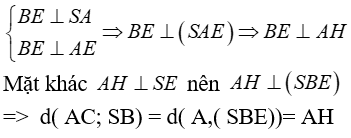 Vì SA ⊥ (ABC) nên hình chiếu của SC bên trên mặt mày phẳng phiu (ABC) là AC suy rời khỏi góc thân thiết SC và mặt mày phẳng phiu (ABC) là ∠SCA = 60°
Vì SA ⊥ (ABC) nên hình chiếu của SC bên trên mặt mày phẳng phiu (ABC) là AC suy rời khỏi góc thân thiết SC và mặt mày phẳng phiu (ABC) là ∠SCA = 60°
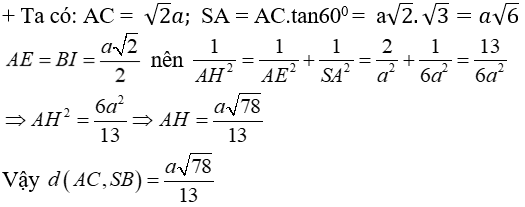
Câu 5:
Cho hình chóp S.ABC với lòng ABC là tam giác cân nặng bên trên A. Gọi H và M thứu tự là trung điểm những cạnh BC và SC; SH vuông góc với (ABC), SA = 2a và tạo ra với mặt mày lòng góc 60°. Khoảng cơ hội thân thiết hai tuyến phố trực tiếp AM và BC là:
Hiển thị điều giải
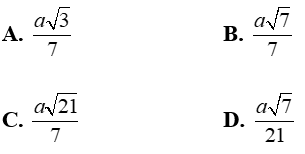
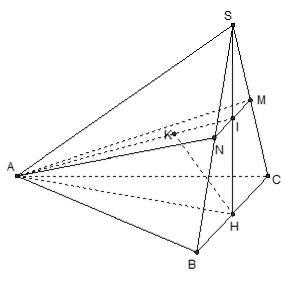 + Hình chiếu vuông góc của SA bên trên mặt mày phẳng phiu (ABC) là HA nên góc thân thiết SA và (ABC) là ∠SAH
+ Hình chiếu vuông góc của SA bên trên mặt mày phẳng phiu (ABC) là HA nên góc thân thiết SA và (ABC) là ∠SAH
⇒ suy rời khỏi AH = SA.cos60° = a; SH = a√3.
+ Gọi N; I thứu tự là trung điểm của SB và SH.
SI = SH/2 = a√3/2
Ta xuất hiện phẳng phiu (AMN) // BC (vì MN // BC)
⇒ d(AM; BC) = d(BC, (AMN)) = d(H; (AMN)).
+ Dựng HK ⊥ AI
 + Xét tam giác IAH vuông bên trên H, đàng cao HK
+ Xét tam giác IAH vuông bên trên H, đàng cao HK
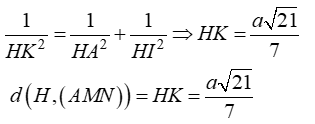 Đáp án C
Đáp án C
Câu 6:
Cho hình chóp S.ABC với lòng ABC là tam giác đều cạnh a, SA vuông góc với mặt mày phẳng phiu (ABC) , gọi I là trung điểm cạnh BC. lõi góc thân thiết đường thẳng liền mạch SI và mặt mày phẳng phiu ( ABC) bởi vì 60°. Khoảng cơ hội thân thiết hai tuyến phố trực tiếp SB và AC
Hiển thị điều giải

 + Hình chiếu vuông góc của SI bên trên mặt mày phẳng phiu (ABC) là AI nên góc thân thiết SI và mặt mày phẳng phiu (ABC) là ∠SIA (vì tam giác SIA vuông bên trên A nên ∠SIA nhọn)
+ Hình chiếu vuông góc của SI bên trên mặt mày phẳng phiu (ABC) là AI nên góc thân thiết SI và mặt mày phẳng phiu (ABC) là ∠SIA (vì tam giác SIA vuông bên trên A nên ∠SIA nhọn)
Suy ra: ∠SIA = 60°.
+ Xét tam giác SIA vuông bên trên A, ∠SIA = 60° và AI = a√3/2 nên SA = AI.tan60° = 3a/2.
+ Dựng hình bình hành ABCD, tam giác ABC đều nên tam giác ABD đều.
+ Ta với AC // BD nên AC // (SBD)
⇒ d(AC; SB) = d(AC, (SBD)) = d(A; (SBD)).
+ Gọi K là trung điểm đoạn BD, tam giác ABD đều cạnh a
suy rời khỏi AK ⊥ BD và AK = a√3/2 nhưng mà BD ⊥ SA nên BD ⊥ (SAK).
+ Dựng AH ⊥ SK, H ∈ SK lại sở hữu AH ⊥ BD suy rời khỏi AH ⊥ (SBD)
Vậy d(A, (SBD)) = AH
+ Xét tam giác SAK vuông bên trên vuông bên trên A, đàng cao AH tớ với
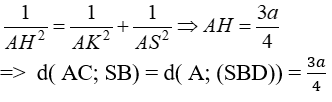 Đáp án B
Đáp án B
Câu 7:
Cho hình chóp S.ABC tam giác ABC vuông bên trên B; BC = a; AC = 2a tam giác SAB đều. Hình chiếu của S lên trên bề mặt phẳng phiu (ABC) trùng với trung điểm M của AC. Khoảng cơ hội thân thiết hai tuyến phố trực tiếp SA và BC là:
Hiển thị điều giải
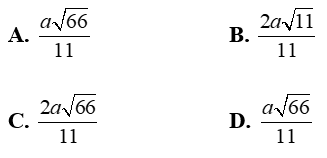
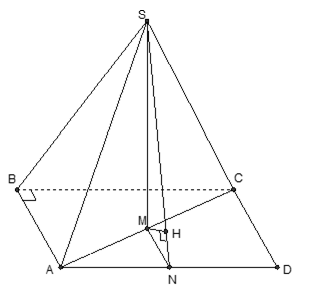 + Tam giác ABC vuông bên trên B, BC = a và AC = 2a suy rời khỏi AB = a√3
+ Tam giác ABC vuông bên trên B, BC = a và AC = 2a suy rời khỏi AB = a√3
Tam giác SAM vuông bên trên M, SA = a√3 ( vì như thế tam giác SAB đều); AM = AC/2 = a ⇒ SM = a√2
+ Dựng hình bình hành ABCD, gọi N là trung điểm của AD. Do ∠ABC = 90° suy rời khỏi ABCD là hình chữ nhật suy rời khỏi MN ⊥ AD.
Lại có: SM ⊥ AD nên AD ⊥ (SMN) .
Dựng MH ⊥ AD, H ∈ SN
Theo bên trên với AD ⊥ (SMN) nên AD ⊥ MH
⇒ MH ⊥ ( SAD).
Vậy d(M; (SAD)) = MH .
+ Do BC // AD nên BC // (SAD)
⇒ d(SA; BC) = d(BC; (SAD) = d(C; (SAD))
= 2d(M; (SAD)) = 2.MH
+ Xét tam giác SMN vuông bên trên M, đàng cao MH:
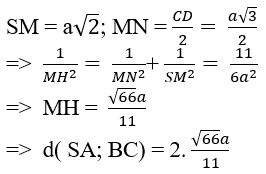 Chọn C
Chọn C
Câu 8:
Cho hình chóp S.ABCD với lòng ABCD là hình thoi cạnh a và ∠ABC = 60°. Hai mặt mày phẳng phiu (SAC) và (SBD) nằm trong vuông góc với lòng, góc thân thiết nhì mặt mày phẳng phiu (SAB) và (ABCD) bởi vì 30°. Khoảng cơ hội thân thiết hai tuyến phố trực tiếp SA và CD bám theo a bằng:
Hiển thị điều giải
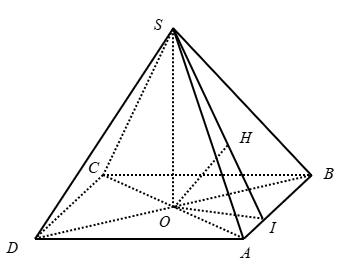 Gọi O là gửi gắm điểm của AC và BD
Gọi O là gửi gắm điểm của AC và BD
Kẻ: OI ⊥ AB; OH ⊥ SI
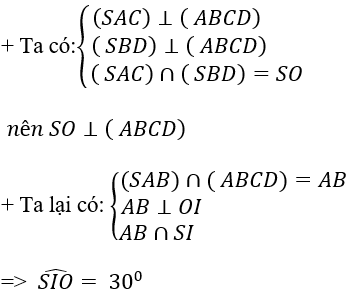 + Do CD // AB nên CD // (SAB)
+ Do CD // AB nên CD // (SAB)
⇒ d(CD; SA) = d(CD, (SAB))
= d(C; (SAB)) = 2d(O; (SAB))
Ta có: AB ⊥ SO, AB ⊥ OI ⇒ AB ⊥ (SOI) ⇒ AB ⊥ OH
Nên OH ⊥ (SAB) ⇒ d(O, (SAB)) = OH
Mà tam giác Ngân Hàng Á Châu cân nặng bên trên B với ∠ABC = 60° nên tam giác ABC đều
⇒ OC = (1/2)AC = (1/2)AB = a/2
+ xét tam giác OAB có:
 Chọn đáp án B
Chọn đáp án B
Câu 9:
Cho hình chóp S.ABCD với lòng ABCD là hình thoi tâm I, AB = 2a ; BD = √3AC, mặt mày mặt SAB là tam giác cân nặng đỉnh A; hình chiếu vuông góc của đỉnh S bên trên mặt mày phẳng phiu lòng trùng với trung điểm H của AI. Khoảng cơ hội thân thiết hai tuyến phố trực tiếp SB và CD bằng:
Hiển thị điều giải
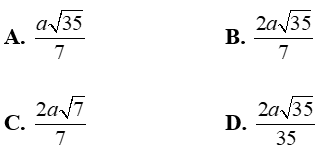
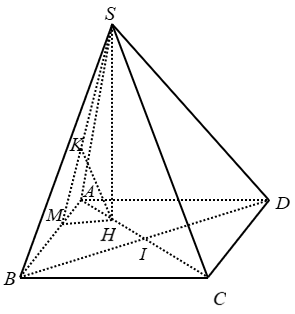 + Ta có: CD // AB ⇒ CD // (SAB)
+ Ta có: CD // AB ⇒ CD // (SAB)
⇒ d(CD; SB) = d(CD; (SAB)) = d(C; (SAB)) = 4.d(H; (SAB))
+ Kẻ MH ⊥ AB; HK ⊥ SM
 Ta có: tan(BAC) = BI/IA = √3 ⇒ ∠BAC = 60° ⇒ ΔABC đều
Ta có: tan(BAC) = BI/IA = √3 ⇒ ∠BAC = 60° ⇒ ΔABC đều
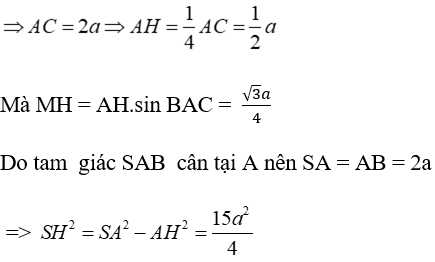 Do đó:
Do đó:
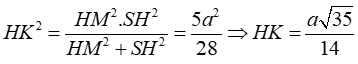
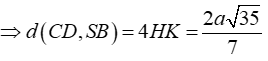
Chọn đáp án B
Câu 10:
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a. Các cạnh mặt mày SA = SB = SC = SD = a√2. Khoảng cách giữa nhì đường thẳng AD và SB là:
Hiển thị điều giải

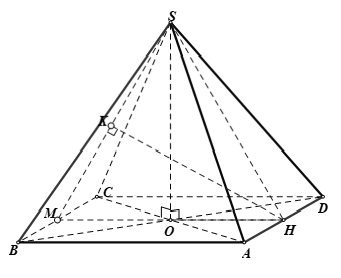 + Do AD // BC nên AD // (SBC)
+ Do AD // BC nên AD // (SBC)
⇒ d(AD; SB) = d(AD, (SBC)) = d(H; (SBC))
Trong bại H là trung điểm AD.
+ Gọi M là trung điểm của BC và K là hình chiếu vuông góc của H lên SM
Xem thêm: Báo VietnamNet
⇒ d(H; (SBC)) = HK.
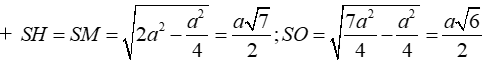 + Diện tích tam giác SMH là:
+ Diện tích tam giác SMH là:
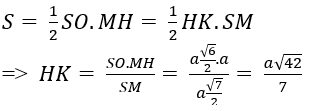 Chọn đáp án C
Chọn đáp án C












Bình luận